机器学习 - 线性回归实验
用scikit-learn和pandas学习线性回归
1. 获取数据,定义问题
我们用UCI大学公开的机器学习数据来跑线性回归。
数据的下载地址在这里:https://archive.ics.uci.edu/ml/datasets/combined+cycle+power+plant 下载后的数据可以发现是一个压缩文件,解压后有一个xlsx文件,用excel打开,另存为csv格式,之后用这个csv格式的文件来运行线性回归。

这是一个循环发电场数据,共有9568个样本数据,每个数据有5列:$AT$(温度)、$V$(压力)、$AP$(湿度)、$RH$(压强)、$PE$(输出电力)。我们不用纠结于每项的具体意义。
我们的问题是得到一个线性的关系,对应PE是样本输出,而$AT、V、AP、RH$这四个是样本特征,机器学习的目的是得到一个线性回归模型,即:
$$
PE= \theta_0+ \theta_1 \times AT+ \theta_2 \times V + \theta_3 \times AP + \theta_4 \times RH
$$
而需要学习的就是$\theta_0,\theta_1,\theta_2,\theta_3,\theta_4$这5个参数。
2. 整理数据
打开这个csv可以发现数据已经整理好,没有非法数据,因此不需要做预处理。但是这些数据并没有归一化,也就是转化为均值0,方差1的格式。(scikit-learn在线性回归时会自动帮我们进行归一化)。
打开JupyterNotebook。在Home页面导入数据集,别忘了点upload上传。然后新建一个Python3笔记。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
|
#导入相关类库
import matplotlib.pyplot as plt #绘图库
#设置插图,让它们在记事本可见
%matplotlib inline
import numpy as np
import pandas as pd
from sklearn import datasets, linear_model
#用pandas读取数据
data = pd.read_csv('ccpp.csv')
data.describe()
#查看数据的前5行
data.head()
#查看数据的后5行
data.tail()
#查看数据的维度
data.shape
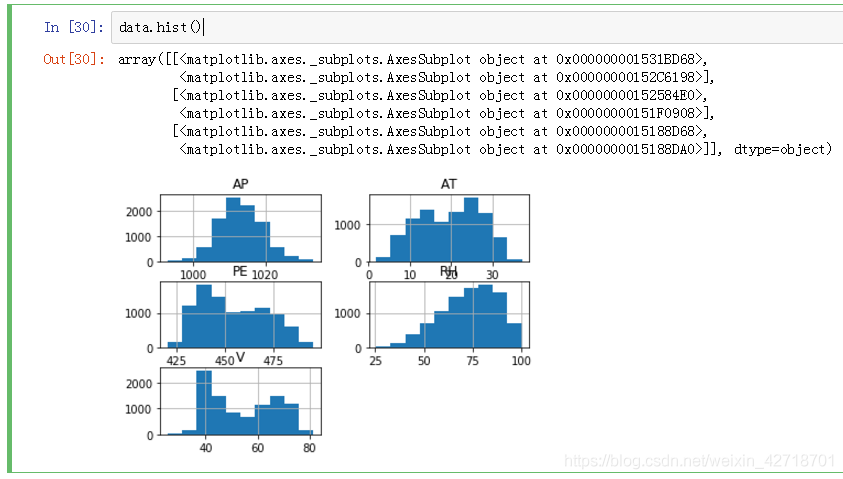
#数据可视化,直方图显示
data.hist()
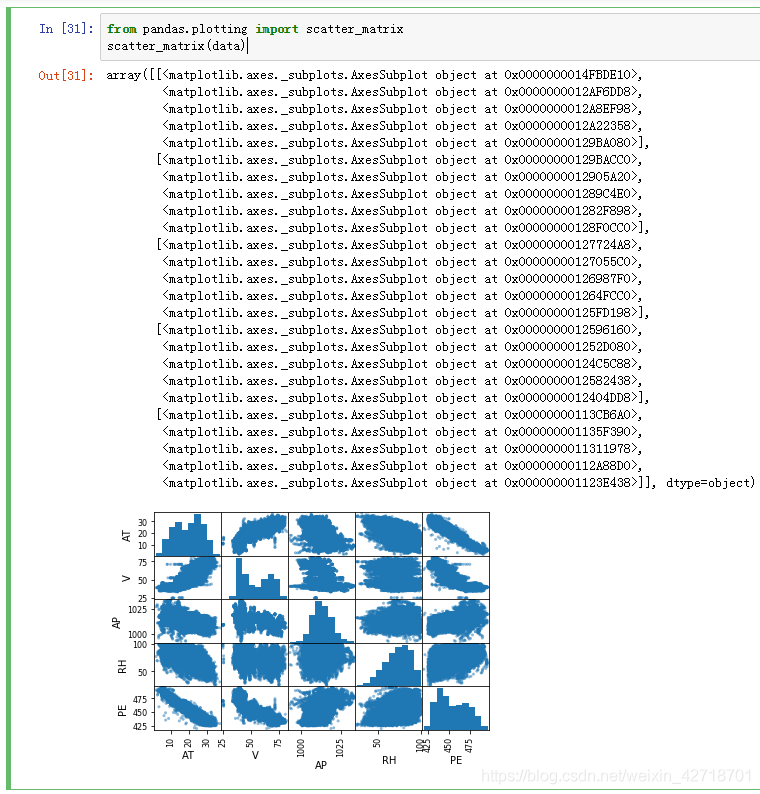
#散点矩阵图
from pandas.plotting import scatter_matrix
scatter_matrix(data)
|
3. 准备数据
该数据集有9568个样本,每个样本有5例。
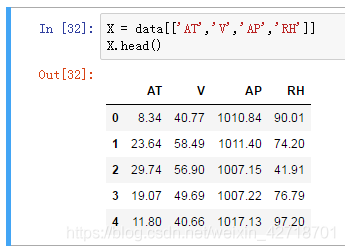
下面我们开始准备样本特征$X$,我们用$AT,V,AP$和$RH$这4个列作为样本特征。
1
2
|
X = data[['AT','V','AP','RH']]
X.head()
|
准备样本输出$y$,我们用$PE$作为样本输出。
1
2
|
y = data[['PE']]
y.head()
|
划分训练集和测试集把$X$和$y$的样本组合划分成两部分,一部分是训练集,一部分是测试集。使用train_test_split函数,官方文档地址:
https://scikit-learn.org/stable/modules/generated/sklearn.model_selection.train_test_split.html#sklearn.model_selection.train_test_split
1
2
|
from sklearn.model_selection import train_test_split
X_train,X_test,y_train,y_test = train_test_split(X, y, random_state=1)
|
参数:
test_size:测试集大小。如果为浮点型,则在0.0-1.0之间,代表测试集的比例;如果为整数型,则为测试集样本的绝对数量;如果没有,则为训练集的补充。默认情况下,值为0.25。此外,还与版本有关。
train_size:训练集大小。如果为浮点型,则在0.0-1.0之间,代表训练集的比例;如果为整数型,则为训练集样本的绝对数量;如果没有,则为测试集的补充。
random_state:指定随机方式。一个整数或者andomState实例,或者None。如果为整数,则它指定了随机数生成器的种子;如果为RandomState实例,则指定了随机数生成器;如果为None,则使用默认的随机数生成器,随机选择一个种子。
shuffle:布尔值。是否在拆分前重组数据。如果shuffle=False,则stratify必须为None。
stratify:array-likeorNone。如果不是None,则数据集以分层方式拆分,并使用此作为类标签。
返回值:拆分得到的train和test数据集。
1
2
3
4
5
|
#查看下训练集和测试集的维度,可以看到75%的样本数据被作为训练集,25%的样本被作为测试集。
print(X_train.shape)
print(y_train.shape)
print(X_test.shape)
print(y_test.shape)
|
4. 训练数据
用scikit-learn的线性模型来拟合我们的问题。
1
2
3
|
fromsklearn.linear_modelimportLinearRegression#普通线性回归模型,使用最小二乘法拟合数据
linreg = LinearRegression()
linreg.fit(X_train,y_train)
|
线性回归fit函数用于拟合输入输出数据,调用形式为$model.fit(X,y,sample_weight=None):
•X:X为训练向量;
•y:y为相对于X的目标向量;
•sample_weight:分配给各个样本的权重数组,一般不需要使用,可省略。
注意:$X$,$y$以及model.fit()返回的值都是2-D数组,如:$a=[[0]]$
1
2
3
|
#拟合完毕后,查看得到的模型参数:
print(linreg.intercept_)
print(linreg.coef_)
|
这样我们就得到了线性回归模型里面需要求得的5个参数值。
5. 模型评价
模型训练完以后,需要评估模型的好坏程度,对于线性回归来说,我们一般用均方差(MeanSquaredError,MSE)或者均方根差(RootMeanSquaredError,RMSE)在测试集上的表现来评价模型的好坏。如果我们用其他方法得到了不同的参数,需要选择模型时,就用MSE小的模型参数。
1
2
3
4
5
6
7
|
#模型拟合测试集
y_pred = linreg.predict(X_test)
from sklearn import metrics
#用scikit-learn计算MSE
print("MSE:",metrics.mean_squared_error(y_test,y_pred))
#用scikit-learn计算RMSE
print("RMSE:",np.sqrt(metrics.mean_squared_error(y_test,y_pred)))
|
尝试用不同的线性模型进行训练
加入正则化项,岭回归模型,L2范数调用Ridge函数同学们手动调整alpha的值,观察结果的变化。思考:alpha值大小跟过拟合、欠拟合的关系?
1
2
3
4
5
|
from sklearn.linear_model import Ridge
rdg = Ridge(alpha=10000,fit_intercept=True)
rdg.fit(X_train,y_train)
print(rdg.intercept_)
print(rdg.coef_)
|
#模型拟合测试集
1
2
3
4
5
6
|
y_pred = rdg.predict(X_test)
from sklearn import metrics
#用scikit-learn计算MSE
print("MSE:",metrics.mean_squared_error(y_test,y_pred))
#用scikit-learn计算RMSE
print("RMSE:",np.sqrt(metrics.mean_squared_error(y_test,y_pred)))
|
套索回归模型,L1范数
调用LASSO函数
1
2
3
4
5
|
from sklearn.linear_model import Lasso
las = Lasso(alpha=0.1)
las.fit(X_train,y_train)
print(las.intercept_)
print(las.coef_)
|
#模型拟合测试集
1
2
3
4
5
6
7
|
y_pred = las.predict(X_test)
from sklearn import metrics
#用scikit-learn计算MSE
print("MSE:",metrics.mean_squared_error(y_test,y_pred))
#用scikit-learn计算RMSE
print("RMSE:",np.sqrt(metrics.mean_squared_error(y_test,y_pred)))
print("迭代次数:",las.n_iter_)
|
交叉验证
我们可以通过交叉验证来持续优化模型,采用10折交叉验证,即cross_val_predict中的cv参数为10:
1
2
3
4
5
6
7
8
|
X = data[['AT','V','AP','RH']]
y = data[['PE']]
from sklearn.model_selection import cross_val_predict
predicted=cross_val_predict(linreg,X,y,cv=10)
#用scikit-learn计算MSE
print("MSE:",metrics.mean_squared_error(y,predicted))
#用scikit-learn计算RMSE
print("RMSE:",np.sqrt(metrics.mean_squared_error(y,predicted)))
|

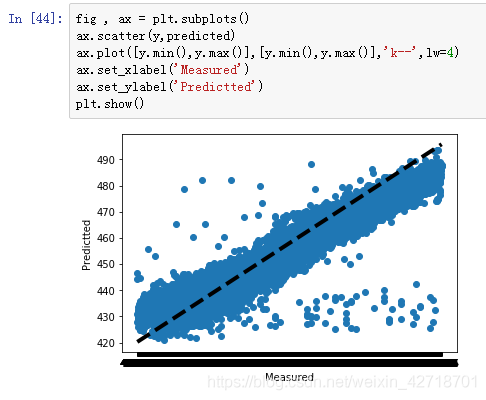
6. 画图观察结果
画图观察真实值和预测值的变化关系,离中间的直线y=x越近的点,代表预测损失越低。
1
2
3
4
5
6
7
|
fig,ax = plt.subplots()
ax.scatter(y,predicted)
ax.plot([y.min(),y.max()],[y.min(),y.max()],'k--',lw=4)
#尝试将k--改为r--,r-,观察线型。查看某个函数的详细信息,使用help()函数。
ax.set_xlabel('Measured')
ax.set_ylabel('Predicted')
plt.show()
|
7. python程序完整源代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
|
import matplotlib.pyplot as plt
%matplotlib inline
import numpy as np
import pandas as pd
from sklearn import datasets , linear_model
data = pd.read_csv('ccpp.csv')
data.describe()
data.head()
data.tail()
data.shape
data.hist()
from pandas.plotting import scatter_matrix
scatter_matrix(data)
X = data[['AT','V','AP','RH']]
X.head()
y = data[['PE']]
y.head()
from sklearn.model_selection import train_test_split
X_train , X_test , y_train , y_test = train_test_split(X , y , random_state=1)
print (X_train.shape)
print (y_train.shape)
print (X_test.shape)
print (y_test.shape)
from sklearn.linear_model import LinearRegression
linreg = LinearRegression()
linreg.fit(X_train,y_train)
print(linreg.intercept_)
print(linreg.coef_)
y_pred = linreg.predict(X_test)
from sklearn import metrics
print("MSE:",metrics.mean_squared_error(y_test,y_pred))
print("RMSE:",np.sqrt(metrics.mean_squared_error(y_test,y_pred)))
from sklearn.linear_model import Ridge
rdg = Ridge(alpha=8000,fit_intercept=True)
rdg.fit(X_train,y_train)
print(rdg.intercept_)
print(rdg.coef_)
y_pred = rdg.predict(X_test)
from sklearn import metrics
print("MSE:",metrics.mean_squared_error(y_test,y_pred))
print("RMSE:",np.sqrt(metrics.mean_squared_error(y_test,y_pred)))
from sklearn.linear_model import Lasso
las = Lasso(alpha = 0.1)
las.fit(X_train,y_train)
print (las.intercept_)
print (las.coef_)
y_pred = las.predict(X_test)
from sklearn import metrics
print("MSE:",metrics.mean_squared_error(y_test,y_pred))
print("RMSE:",np.sqrt(metrics.mean_squared_error(y_test,y_pred)))
print("迭代次数:",las.n_iter_)
X = data[['AT','V','AP','RH']]
y = data[['PE']]
from sklearn.model_selection import cross_val_predict
predicted = cross_val_predict(linreg , X , y , cv=10)
print("MSE:",metrics.mean_squared_error(y,predicted))
print("RMSE:",np.sqrt(metrics.mean_squared_error(y,predicted)))
fig , ax = plt.subplots()
ax.scatter(y,predicted)
ax.plot([y.min(),y.max()],[y.min(),y.max()],'k--',lw=4)
ax.set_xlabel('Measured')
ax.set_ylabel('Predictted')
plt.show()
|





